1. The Guitar Construction & Function
1.1 Introduction
The guitar is a stringed instrument that has it’s roots way back in the ancient world but was first acknowledged as a concert instrument during the 19th century. We can divide today’s guitar into four main types, i.e. the Classical guitar (nylon-string guitar), the Acoustic guitar (steel-string guitar), the archtop guitar (Jazz guitar) and the Electric guitar where the first three do not need any extra amplification.
However, regardless of type, they have a couple of things in common. All guitar types are equipped with strings that are attached to the bridge (at the guitar body) and to the tuning machines (at the guitar headstock). To get the guitar to sound the strings are either strummed or plucked. Figure 1.1 illustrates the name of the different main parts of the guitar.
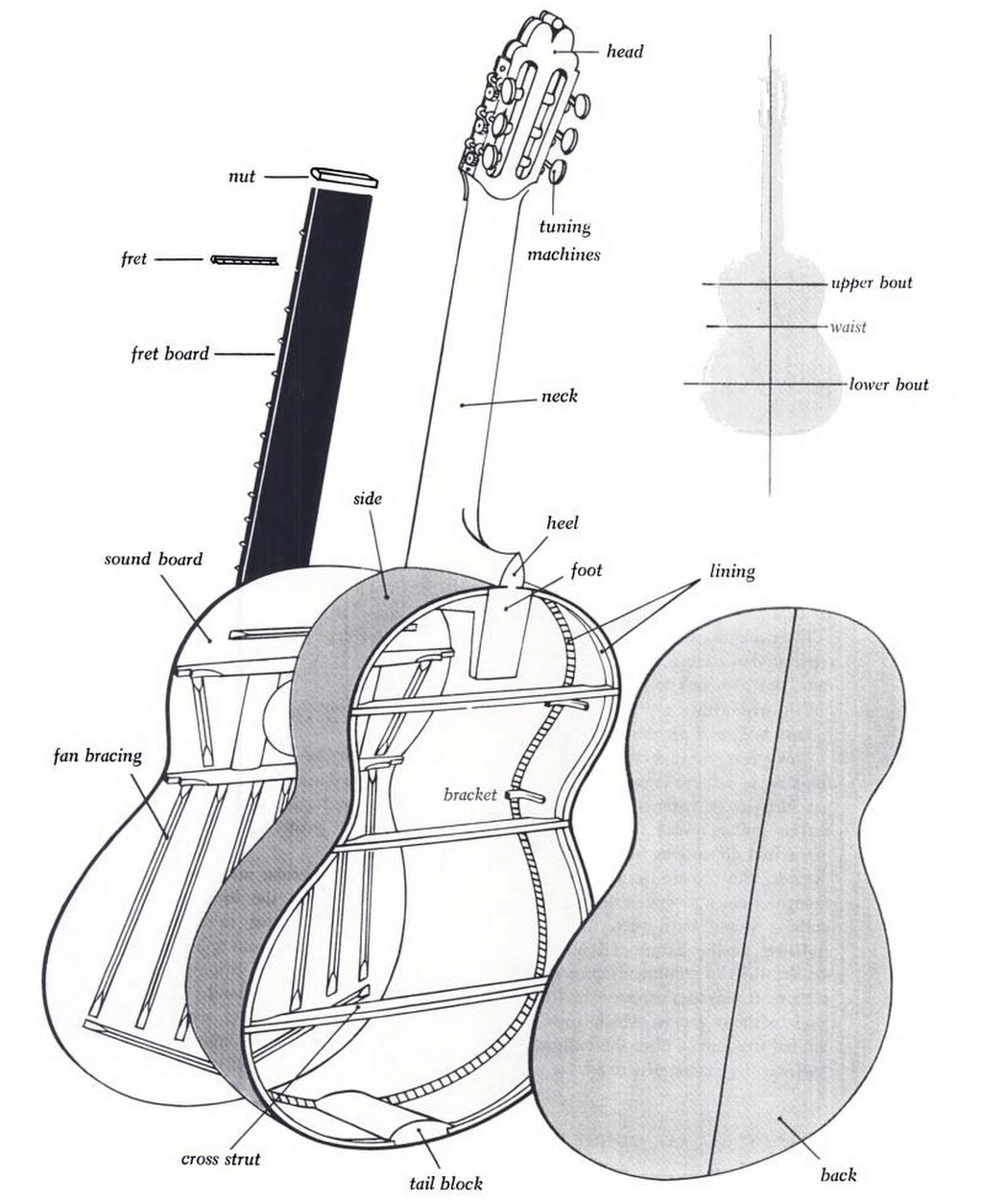
Figure 1.1Exploded view of the classical guitar. (Sloane 1976)
1.2 The Strings
The strings are often tuned to “standard tuning” which defines the pitches E A D G B E from the lowest (thickest) to the highest (thinnest). The nonstandard tunings are called “alternate” or “alternative” and many of these are easier understood and easier to master when taking standard tuning as a starting-point. There are hundreds of ways you can tune a guitar and most of them are found in our smartphone app. A common way to differentiate each string is to use numbering. For a six-stringed guitar the thinnest string is called the first (1st) and then the number increment for each string. Hence the thickest is called the sixth (6th) string. Note, do not confound this by the numbering that describe the octave. You can read more about guitar tuning here.
1.3 The Guitar Neck
The neck is desirably made of stiff and stable wood to resist the string tension. Commonly used wood are Mahogany, Spanish Cedar, Maple and Walnut.
1.3.1 The Tuning Machines
To make it possible to tune each string the neck is fitted with tuning machines that is constructed to adjust the tension. The greater force that pull the string the faster the string will vibrate and therefore generate a higher frequency. The pitch is also depending on the scale length (string length) and the mass per unit length (string thickness and density). A short and thin string which is pulled by a greater force will result in a high frequency and the other way around. The mathematics that describe this phenomena is explained by equation 1.1 and it can be used to calculate the fundamental frequency of a string (the first resonance mode).
$$ f_0 = \frac{1}{2L}\sqrt{\frac{T}{\mu}} $$Equation 1.1The fundamental frequency of a string.
We can do some calulation from some known values to better understand that this mathematic expression really works. Let us assume that we have a \(650 mm\) long string with the radius of \(1 mm\), made of a material with the density of \(1150 kg/m^3\) and that is tuned to a tension of \(41.47 Newton\) (this force corresponds to the force caused by a mass of 4.2kg on earth). The fundamental \(f_0\) will then be:
$$ f_0 = \frac{1}{2\cdot0.65} \sqrt{\frac{41.47}{1150\cdot0.001^2\cdot\pi}}\\ \;\\ \Rightarrow\\ \;\\ f_0 = 82.4 Hz $$Example 1.1Calculation example of a guitar string. The numbers are doctored to give the frequency of the thick E-string, i.e 82,4Hz.
This is just some basics how to calculate the fundamental frequency of a scientifically perfect string. In reality it is much more complicated and the human perception is of big importance. I will cover the science and perception of the fundamental frequency in another article. We can live with this explanation for now and see how the guitar player modifies the pitch by changing the value L in Equation 1.1.
1.3.2 The Fretboard
The fretboard need to stand all wear and tear for years of playing and is commonly made of the hardwoods Ebony or Rosewood . To make it easier to play notes and chords the fretboard is supplied with frets. When a string is pushed to a fret the string length will get shorter and therefore result in a higher pitch (described above).
Classical guitars often have 19 frets and acoustic guitars has usually 21 frets. The 12th fret is always placed at half the scale length, i.e in the middle between the nut and the bridge saddle. Hence, the corresponding pitch will equal twice the pitch of the full string length which in musical terms means one octave up. For example, if you play the tuned 6th (thickest) string it will have a pitch called E2. The number 2 here describes the actual octave. This equals 82,4Hz (Hz = Hertz = oscillations per second). When you play this string at the 12th fret it will give you the double frequency and the pitch called E3. You can experiment with the value of the string length L in Example 1.1 to see how the equation works. When using our guitar tuner you can see that it also detect and display the octave as a subscripted number.
1.3.2.1 The Fret Position
Every fret is positioned to shorten the string and increase the pitch by one semitone. In an equal tempered scale (used in guitars and western music) one octave is divided into 12 semitones where each of them have the same relationship. The ratio between two semitones can be derived from the twelfth root of two, which is about 6 percent. For the inquisitive reader I will explain what this means in a bit but first I will show some approximations how the fret positions could be calculated. If you just want to know the formula to calculate the fret positions please see Equation 1.8 below.
Rule of 18
Historically luthiers have used the rule of 18 because of it's simplicity. The fret position that will increase the pitch by one semitone is calculated from the string length divided by 18, i.e:
$$ x = \frac{L}{18}$$Equation 1.2Rule of 18 fret position formula. Where x describes the distance to the next fret and L the remaining string length.
Back in the days Luthiers used this only because it was easy to calculate by hand. The access to calculators and futhermore computers gave luthiers tools to use a more precise constant. Today, fret position calculations are often made with the constant 17.817. Later I will explain where this magic number comes from.
$$ x = \frac{L}{17.817}$$Equation 1.3A better approximation of the fret position with today's standard constant.
Let us continue to do some calculation with this simple equation and why not continue with the same scale length \(L\) as above, i.e a distance between the nut and bridge saddle of 650mm.
$$ x_{nut \rightarrow fret1} =\frac{L}{17.817} =\\ \;\\ =\frac{650 mm}{17.817} \approx 36.48 mm $$To calculate the second fret position we change our measuring point to the distance between the first fret and the bridge saddle. You can imagine that we have reduced the scale length.
$$ L_2 = L - x_{nut \rightarrow fret1} =\\ \;\\ = 650 - 36.48 = 613.52 mm $$Hence the distance between the first fret and the second fret will be:
$$ x_{fret1 \rightarrow fret2} =\frac{L_2}{17.817} =\\ \;\\ = \frac{613.52}{17.817} \approx 34.44 mm $$We could continue in this way to calculate all fret positions but this will cause an error that grows for every fret. Firstly, due to the fact that we mathematically rounded off the first calculated distance as a two decimal point number. Secondly, even if we make a spreadsheet and keep the accuracy of every calculation it will cause an growing error when in practice measuring the fret. This error comes from the accuracy limit in our measurement tools and in the imperfection of the human that uses these tools. Even if your have super skills and uses some expensive high accuracy measurement tool, it is not good enaugh. The first frets would be perfectly fine but the problem will occur later. Imagine that each fret have a memory and that every new fret position will "remember" and be impacted by all of the small errors you made earlier, i.e the error gets accumalated. To solve this, we need a formula that gives us the distance to each fret from a fixed point. A good idea is to start from fret zero (the nut).
Let us summarize where we are. We now know how to calculate the distance \(x_{nut \rightarrow fret1}\) and \(x_{fret1 \rightarrow fret2}\). That means that the distance from the nut to the second fret becomes:
$$ x_{nut \rightarrow fret2} = x_{nut \rightarrow fret1} + x_{fret1 \rightarrow fret2} $$Let us now define \(n\) as the fret number and the number 17.817 as the constant \(C\), then the distance \(x_{n}\) from the nut to the nth fret will become:
$$ \boxed{ \;\\ \quad x_{n} = x_{n-1} + \frac{L - x_{n-1}}{C}\\ \;\\ \quad where \quad \cases{n > 0,\\ x_0 = 0,\\L = Scale \; length\\C = 17.817} \quad \;\\} $$Equation 1.4A general formula to calculate the nth fret position from the nut
So, is this approximation good enaugh to obtain correct pitch? The answer is both yes and no. It is good enaugh for the majority and is the industry standard to position the frets but stretching and inharmonicity will create some problem. There are different ways to improve the accuracy and Luthiers commonly compensate the bridge and possibly the nut position. Some companies does even provide fretboards with bent frets to enable a "dynamic" fret position for each note. I will discuss the pros and cons further in an article covering intonation.
To sum up, you can use this formula in a spreadsheet like Excel to make your fret calculations for a series of frets and if you want to modify the constant \(C\). However, the equation is not that handy if you directly want to know the distance to a random fret \(n\).
The 12th root of 2
I mensioned above that I would describe where the "magic" constant came from. Well, it is actually nothing magic about this at all. But first, we need some understanding about the equal temperament scale. In a couple of centuries and still today the western music have used a system called twelve-tone equal temperament, short 12-TET. Basically, the system is limited by the octave ratio (2 times the reference). Usually the reference is an A with the frequency of 440Hz. Hence the octave is an A of 880Hz. In a twelve-tone system the octave interval is divided into twelve discrete parts, the notes. In the equal tempered scale the notes are equally spaced on a logaritmic scale. Therefore, the frequency ratio between any two adjacent notes must be the same. In a mathematic language this ratio is expressed as \(\sqrt[12]{2}\) (the 12th root of two).
If you are not familiar with the root expression or have forgotten what it means I will update you. Let us define a random number called \(z\). The root of \(z\) is then expressed as \(\sqrt{z}\). Implicitly, it means the 2nd root of \(z\), often called the square root and can be written as \(\sqrt[2]{z}\). In words, this expression is the same as the question; What number multiplied by itself 2 times will result in the number \(z\). If we replace the number 2 with a number called \(p\) we can write a more general expression as \(\sqrt[p]{z}\). In words the corresponding question would be; What number multiplied by itself \(z\) times will result in the number \(z\). We define the answer to that question as \(y\) and write the complete equation.
$$ y = \sqrt[p]{z}\\ or\\ y = z^\frac{1}{p} $$To implement this reasoning to our case with the equal temperament scale we can conclude that the 12th root of 2 will give us the ratio \(y\) that 12 times itself will become 2 and equally describe the ratio between two adjacent semitones. In other words, the 12th root of 2 is exactly the same as 2 raised to the 1/12th power.
$$ y = \sqrt[12]{2} = 2^\frac{1}{12}\\ y = 1.05946309436 $$Equation 1.5The ratio between two adjacent semitones in the 12-TET system.
As you can see in Equation 1.5 the ratio between two adjacent notes is no more than approximatically 6 percent. From the discussion above we can define the interval \(y\) between \(n\) semitones as.
$$ \boxed{\;\ \\ \quad y = 2^\frac{n}{12} \quad \\ } $$Equation 1.6The relationship between \(n\) semitones in the 12-TET system.
From Equation 1.1 we concluded that the fundamental frequency was directly proportional to the string length \(L\). Now when we know what the ratio \(y\) is between the semitones we can use this to calculate the string length \(L_2\) that will be one semitone above the reference string length.
$$ L_2 = \frac{L}{y}\\ $$Thereby, the distance \(x\) between the nut to the first fret will become:
$$ x_{nut \rightarrow fret1} = L - L_2 = \\ \;\\ = L - \frac{L}{y} = L(1 - \frac{1}{ 2^\frac{1}{12}})\\ \;\\ \Rightarrow\\ \;\\ x_{nut \rightarrow fret1} = L(1 - 2^\frac{-1}{12}) $$From the Rule of 18 we also know that the distance \(x_{nut \rightarrow fret1}\) was defined as \(\frac{L}{C}\). Now let us put that information together and discover what will happend.
$$ L(1 - 2^\frac{-1}{12}) = \frac{L}{C}\\ \;\\ \Rightarrow\\ \;\\ C = \frac{1}{1 - 2^\frac{-1}{12}} = 17.8171537451 $$Equation 1.7Calculation of the Rule of 18 constant.
Voila! We have now proved where the "magic" constant is derived from and when we know that it is no need to use the hardcoded number 17.817 any more. Instead, we can can make a formula that works out of the box with help of the twelfth root of two. To calculate the distance between any fret to the bridge and to the nut we now have these two simple formulas.
$$ \boxed{ \;\\ \quad x_{fret[n] \rightarrow bridge} = L \cdot 2^\frac{-n}{12}\\ \;\\ \quad x_{fret[n] \rightarrow nut} = L(1 - 2^\frac{-n}{12})\\ \;\\ \quad where \quad \cases{n = fret \; number\\ L = scale \; length} \quad \;\\} $$Equation 1.8Formulas to calculate any fret position to the bridge and to the nut for the 12-TET scale.
The Equation 1.8 works to calculate the fret positions for any fretted stringed instrument that uses the 12-TET. With just a small modification the formulas works with any equal tempered scale. The only thing you need to do is to change the number 12 to whatever tone system you desire.
In the next article here on ProGuitar I will write about the contruction and function of the Guitar body
